Activation Functions
线性可分 VS 线性不可分
在讨论激活函数之前，我们应该先了解为什么激活函数是有必要存在的. 对于线性神经网络，可以表示为 \[y = Wx + b\] 无论隐藏层有多少、隐藏节点有多少，线性神经网络的本质上依旧是线性的组合. 这样的神经网络理论上可以通过寻找空间中超平面的方式来解决线性可分的问题： 
但是对于一些稍微复杂的问题，线性分类器就无法找到一条直线(超平面)去划分出不同的类别：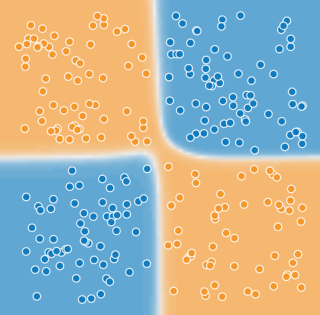 
同样的，对于回归问题，当因变量和自变量之间的关系无法简单用一条直线描述时，线性神经网络的效果就非常差了.
激活函数
对于上面说到的线性神经网络无法解决非线性分类和回归的问题，可以通过加入激活层来引入非线性因素，本质上是每个节点的输出在加权和的基础上做了一个分线性变换： \[y = Activation(Wx + b)\]
经典的损失函数
Sigmoid
Sigmoid 函数本身的表达非常简单： \[g(x) = {1 \over {1+e^{-x}}}\] 而且其求导也非常方便(derivates of sigmoid function)： \[g'(x) = {e^{-x} \over {(1+e^{-x}})^2} = g(x)(1-g(x))\]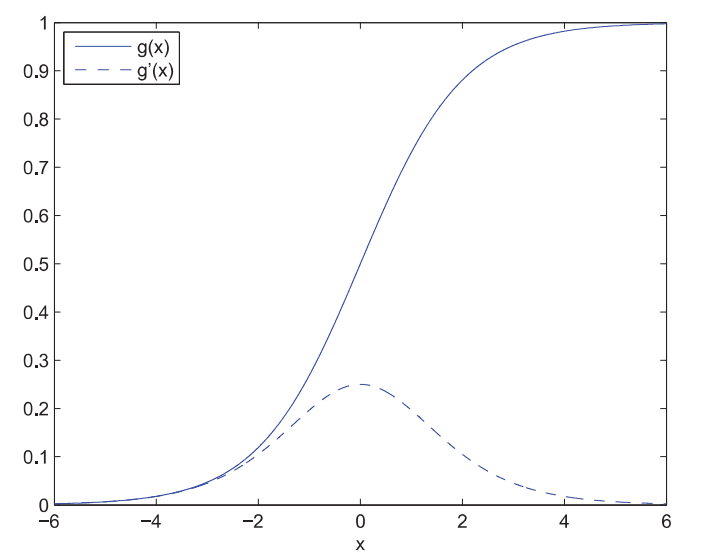 
Sigmoid 函数可以将任意的输出值转换到\([0, 1]\)之间且\(f(0)=0.5\)，因此在分类问题中很适合作为概率值.
然而Sigmoid函数有它的局限性，从上图中可以看出，当自定义值超过一定范围后，其导数值趋近于零，这将会导致神经网络前几层起不到太大的作用，俗称「梯度消失」(vanishing gradient). 一般来说当神经网络超过5层时梯度消失问题就可能会出现. 而且Sigmoid函数的导数涉及除法，计算量相对较大；其敏感区间较短(-1,1)，超过该范围则进入饱和区间(saturation area).
Tanh
双曲正切函数(Hyperbolic Tangent) 是双曲正弦函数和双曲余弦函数的比值： \[tanh(x) = {sinh(x) \over cosh(x)} = {e^x - e^{-x} \over e^x + e^{-x}}\] Tanh函数可以由Sigmoid函数变换得出： \[tanh(x) = 2sigmoid(2x)-1\] 这个函数从图像上看很像是对Sigmoid的一种缩放，而且Tanh函数是关于原点对称的，相比Sigmoid可以提高训练效率，因为其输出更容易接近均值(0). 但它并没有解决Sigmoid中vanishing gradient 和 calculating cost 的问题. \[tanh'(x) = {4e^{-2x}\over (1+e^{-2x})^2}\]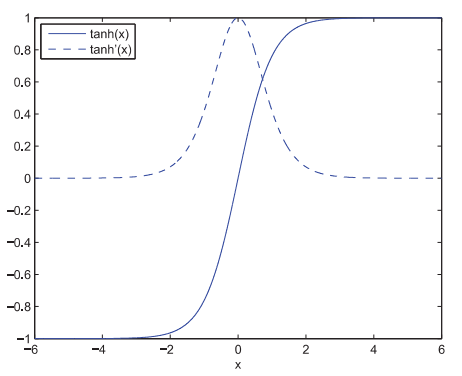 
Relu
根据神经科学的研究发现，人脑的神经系统偏稀疏？(The operating mode of the neurons has the characteristic of sparsity)，仅有1%-4%的神经元会在传递中被同时激活. 但在前面提到的两种激活函数中，大概会有50%的神经元会被同时激活.
线性修正单元，ReLU(Rectified linear units)的定义就要简单许多： \[g(x) = max(0, x) = \begin{cases}
x& x \ge 0 \\
0& x \le 0
\end{cases}\] 其导数也十分简单： \[g'(x) = = \begin{cases}
1& x \ge 0 \\
0& x \le 0
\end{cases}\] 当\(x \ge 0\)时其导数为一个常数，这样就解决了vanishing gradient problem.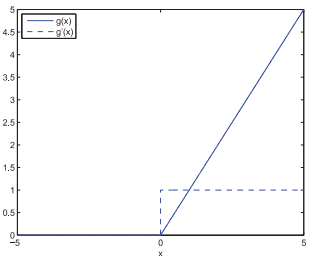 
而且ReLU还有以下这些优点：
- 因为函数简单，不涉及除法和幂运算，计算速度会得到提升；
- 因为梯度在持续下降，因此ReLU也会使损失函数更快速的converge；
- 可以使神经网络更容易获得稀疏的表达. 因为有更多的0；
- 因为导数是常数，所以可以避免陷入local optimization；
- Deep neural networks with ReLU activation functions can reach their best performance without requiring any unsupervised pre-training on purely supervised tasks with large labeled datasets. (这句不太理解，cited from 'Activation Functions and Their Characteristics in Deep Neural Networks')
但是当\(x \le 0\)时，这部分值的神经元永远不会被激活；而且经过ReLU的数值平均值是一个positive value，也就是说下一层接收到的inputs永远都是正数. 这两个问题都会对神经网络的收敛造成影响.
针对上面的问题，LReLU(leaky rectified linear units)进行了改进： \[g(x) = max(0, x) = \begin{cases} x& x \ge 0 \\ 0.01x& x \le 0 \end{cases}\] 所以导数也就变成了： \[g'(x) = = \begin{cases} 1& x \ge 0 \\ 0.01& x \le 0 \end{cases}\]
在上式中，如果用\(a\)替换掉\(0.01\)，那这个函数就被成为PReLU. 还有一种针对ReLU的improvement，RReLU(random)就是在训练的时候每次从uniform distribution中选一个值作为\(a\)，a~U(0,1)，然后在测试时，把参数设置成0.5.
ELU
为了能够将激活层输出的均值尽可能的靠近均值(0)，有人提出了一种ELU(exponential linear unit)函数(\(\alpha > 0\))： \[g(x) = = \begin{cases} x& x \ge 0 \\ \alpha (e^x -1 ) & x \le 0 \end{cases}\] the derivative function is： \[g'(x) = = \begin{cases} 1& x \ge 0 \\ \alpha e^x & x \le 0 \end{cases}\]
函数图像如下所示：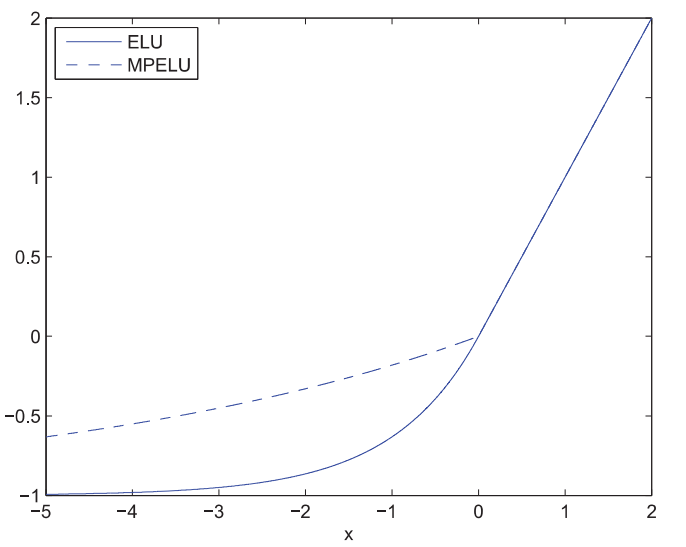 
其中参数\(\alpha\)的作用是使激活函数的负定义域部分保持饱和，这样的设计可以使网络becomes more robust. 因为激活函数的右半部分的导数是一个constant，因此vanishing gradient问题也得到了缓解.
Swish
\[f(x) = x · sigmoid(\beta x)\]
Maxout
Maxout函数的定义为： \[g(x) = max(w_1^Tx+b_1, w_2^Tx+b_2)\]
The Maxout activation is a generalization of the ReLU and the LReLU functions. It is a learnable activation function. Maxout是一个分段线性函数，返回的是输入中的最大值.
好吧，这个函数我没太搞懂...