Distribution 相关 (待补充)
正态分布
正态分布/高斯分布 (Normal Distribution/Gussian Distribution) : \[f(x) = {1\over \sigma \sqrt {2\pi}} e^{-{(x-\mu)^2 \over 2\sigma^2}}\] 记作 \(X\)~\(N(\mu,\sigma^2)\),其中 \(E[x] = \mu, V[x] = \sigma^2\),标准正态分布记作 \(X\)~\(N(0,1)\)
伯努利分布
伯努利分布 (Bernoulli Distribution) 用于离散二元随机变量的分布 (discrete binary) : \[p(x|\theta) = \theta^x(1-\theta)^{1-x}\] 其中 \(E[x] = \theta, V[x] = \theta(1-\theta)\)
二项分布
二项分布 (Binomial Distribution) 其实是伯努利分布的一种延申,当实验次数大于1次时,可表示为 : \[p(x|n, \theta) = \left( \begin{matrix} n\\ x\end{matrix}\right) \theta^x(1-\theta)^{n-x}\] 其中 \(E[x] = n\theta, V[x] = n\theta(1-\theta)\) 当 \(n\) 足够大时,二项分布接近于泊松分布 : \[p(x|\lambda) = {\lambda^x \over x!}e^{-\lambda} , \lambda = n\theta\]
泊松分布
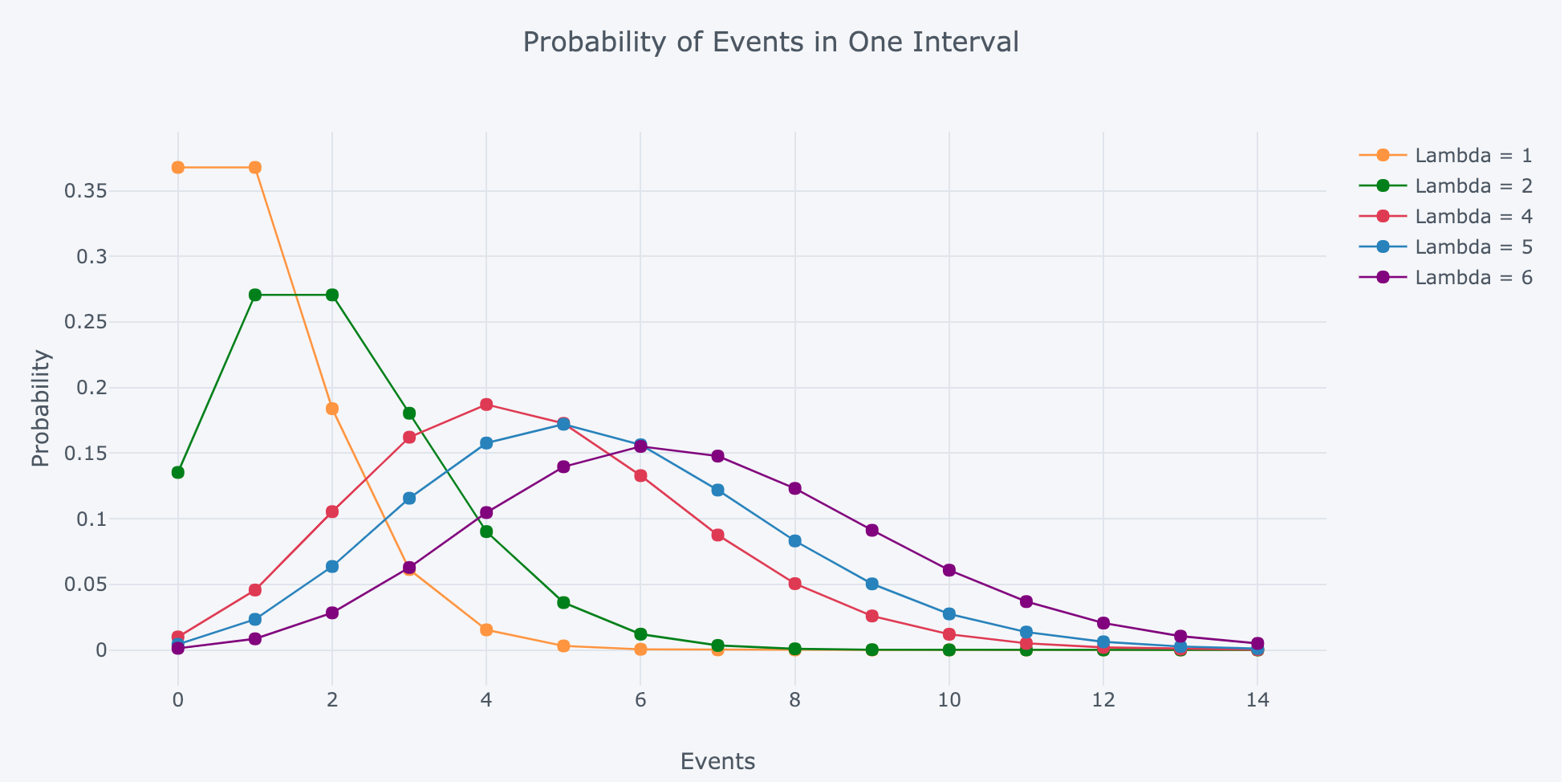
泊松分布 (Poisson Distribution) 是一种离散分布,适合于描述单位时间内随机事件发生的次数的概率分布: \[p(x|\lambda) = {\lambda^x \over x!} e{-\lambda}\] 其中 \(E[x] = \lambda, V[x] = \lambda\),the Poisson distribution is an example of a distribution in which the variance grows with the mean. If \(X\) ∼ \(Pois(λ_X )\) and \(Y\) ∼ \(Pois(λ_Y )\) then \((X + Y)\) ∼ \(Pois(λ_X + λ_Y)\)
中心极限定理
中心极限定理 (Central Limit Theorem) 说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布. 这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件.
- 对于二项分布,当 \(n\) 足够大时,变量和分布趋近于正态分布,for large \(n\), and \(nθ\), \(n(1 − θ)\) not too small, \(M\) ∼ \(Bin(θ, n)\) approaches \(N(nθ, nθ(1 − θ))\)
- 对于泊松分布,当 \(\lambda\) 足够大时,变量和分布趋近于正态分布,\(n\) ∼ \(Pois(λ)\) approaches \(N(λ, λ)\) for large \(λ\), Poisson is skewed to the right (泊松分布是一种右偏分布)
随机变量 \(X\) 的偏度 \(γ1\) 为三阶标准矩 : \[γ1 = E[({x-E[x] \over \sqrt V[x]})^3] = E[({x-\mu \over \sigma})^3] = {\mu^3 \over \sigma^3}\]
关于标准矩 (standard normalization) : 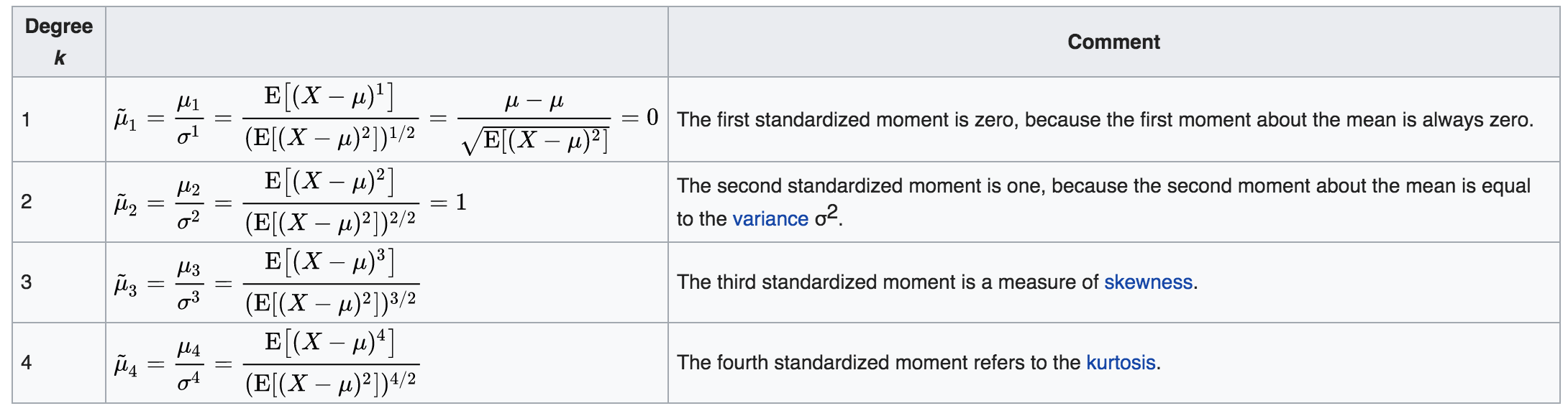
Generally, have distribution with mean \(µ\) and variance \(σ^2\) , and sample n identical RVs \(x_1, ... , x_n\) from it. Then the sample mean \({1 \over n} \sum_{n}^{i=1} x_i\) is approximately distributed as \(N(µ, {1 \over n} σ^2)\) for large \(n\).