ROC and AUC

Posted on | Post modified:
Words count in article: 878 | Reading time ≈ 5

ROC & AUC

Confusion Matrix

I am going to introduce the concept of Confusion Matrix before talking about the ROC as well as AUC since I think this will help us to understand them better. Confusion Matrix is a performance measurement for machine learning classification, which is a specific table layout. Let us undetstand TP, FP, FN and TN first. confusion_matrix As the above picture show, we define them as:

  • TP(True Positive): The samples which are positive and have been predicted as positive

  • FP(False Positive): The samples which are negative but have been predicted as positive

  • FN(False Negative): The samples which are positive but have been predicted as negative

  • TN(True Nagetive): The samples which are negative and have been predicted as negative

So we can calculate the Recall and Precision easily. Recall means out of all the positive classes, how much we predicted correctly: \[Recall = {TP\over{TP + FN}}\] Precision means out of all the classes, how much we predicted correctly: \[Precision = {TP\over{TP + FP}}\] And we can also use F-Score (F1 or F-Measure), which can measure recall and precision simultaneously. F-Score is the harmonic mean of recall and precision: \[F_1 = ({Recall^{-1}+Precision^{-1}\over{2}})^{-1} ={2*Recall*Precision\over{Recall + Precision}}\] \[F_\beta = (1+\beta^2)*{Precision*Recall\over{(\beta^2*Precision)+Recall}}\] Where β is the weight of F-Score, it will give more proportion to Precision when β < 1 and Recall gets a higher proportion when β > 1, β = 1 is a specific situation which Recall and Precision has the same weight. However, it is difficult to compare two models with low precision and high recall or high precision and low recall since their F-Score could be similar. Here we have another two names: Sensitivity and Specificity: \[Sensitivity = Recall = True Positive Rate (TPR)\] \[Specificity = 1 - False Positive Rate (FPR) = 1 - {FP\over{FP + TN}}\] We can try to understand these from conditional probability aspect. Assume that our predict vales is Y' and Y is the true vale, so that: \[Precision = P(Y=1|Y'=1)\] \[Recall = Sensitivity = P(Y'=1|Y=1)\] \[Specificity = P(Y'=0|Y=0)\] It can be seen that Recall (Sensitivity) and Specificity do not be influenced by imbalanced data but Precision relies on the proportion of positive and negative samples.

The Precision-Recall Curve

What's the problem of accuracy?

Accuracy is one of the most common evaluation methods in machine learning, but it is not always appropriate: assume we have 100 samples in the test set, and there are 99 negative samples and just 1 positive sample, so that the accuracy of my model is 99/100 = 99% if it predicts all samples as negative class. Obviously, it can not evaluate our model in this case. \[Accuracy = {TP + TN\over{TP+TN+FP+FN}}\]

What is ROC?

ROC(Receiver Operating Characteristics) curve is a kind of tool which we can use to check or visualize the performance of the multi-classification models. ROC is based on confusion matrix which use FPR as x-axis and TPR as y-axis. We go through all the thresholds and draw the ROC graph, so that each points in ROC represents the FPR and TRP value in a specific threshold.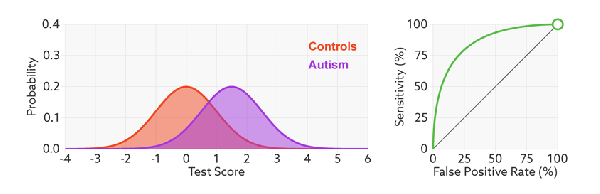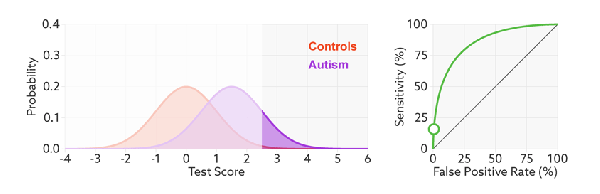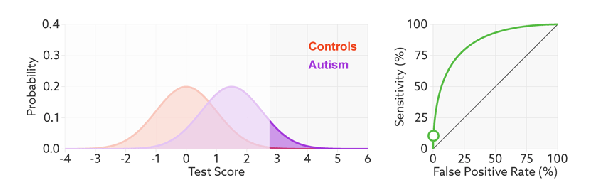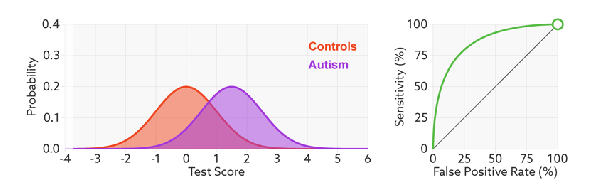

How to evaluate ROC?

The ROC will not change even we modify the threshold, the x-axis, FPR value can be understand as how much we predicted negative samples as positive which should be lower, and the y-axis, TPR value is how much we predicted correctly in the positive samples which should be higher, therefore, the performance of a model is good with high TPR and low FPR, which reflects as a steep ROC curve (The curve should tend to upper left corner). 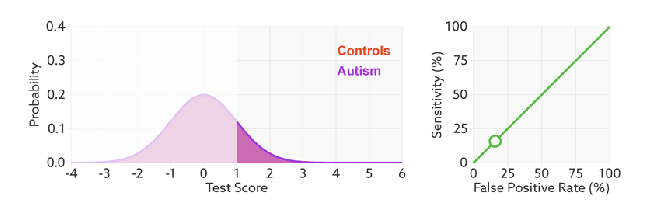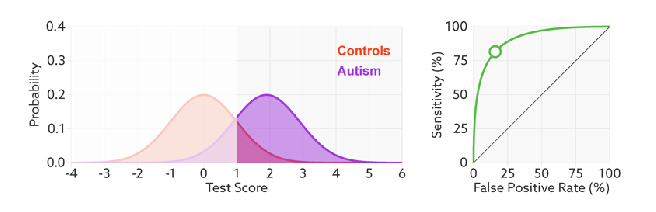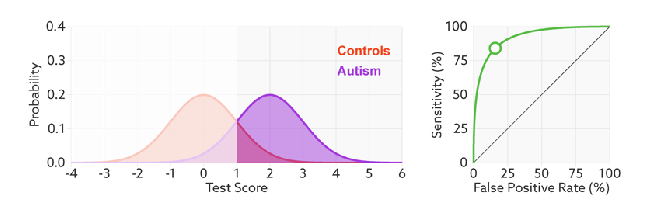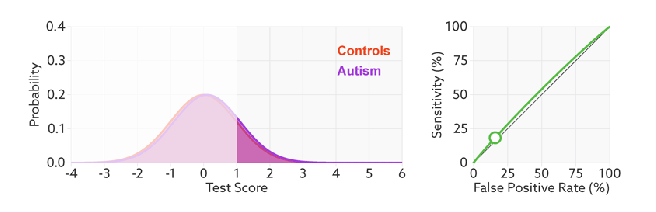In addition, as we said Recall (Sensitivity, TPR) and Specificity (1-FPR) do not be influenced by imbalanced, so ROC curve will also not influenced by imbalanced data: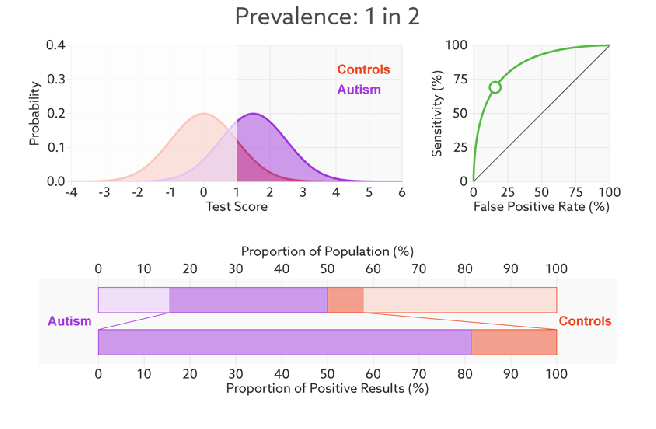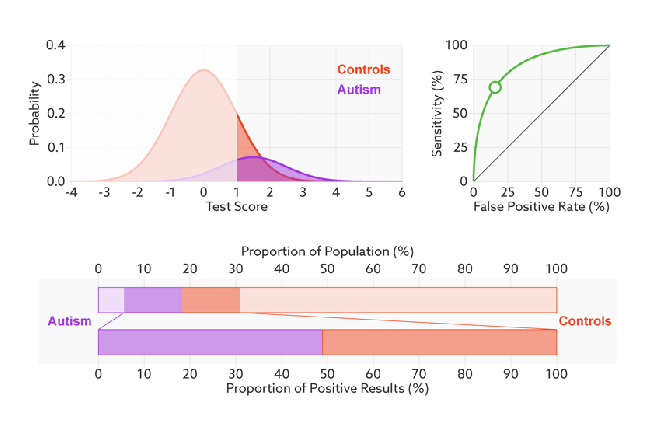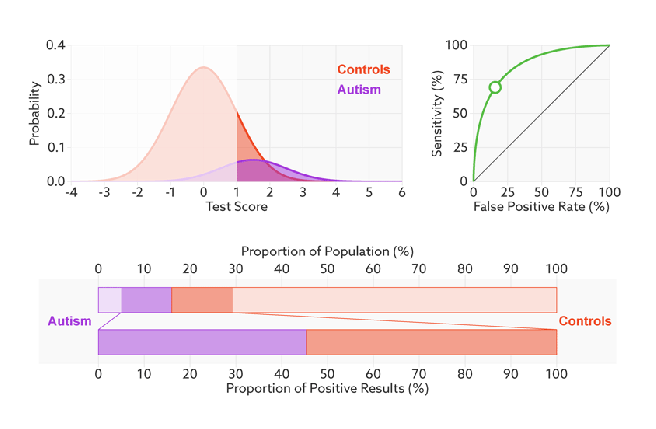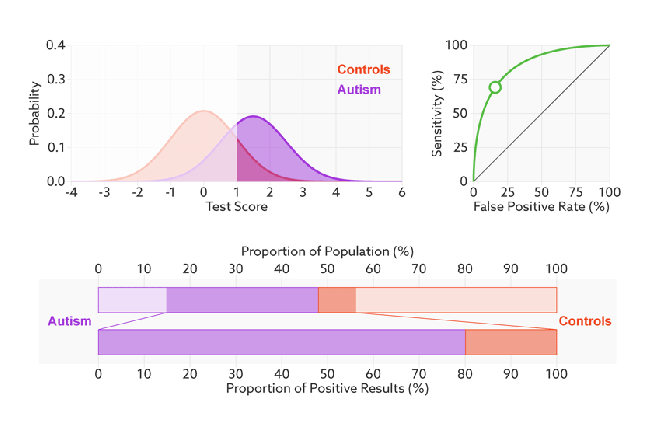

What is AUC?

AUC (Area Under the Curve) is the area under the ROC curve, the diagonal represents random effect which value is 0.5, positive and negative samples occupy the same proportion is the data set in this specific situation. The best value of AUC is 1 but can not reach in the most situation, and the worst is 0.5 which means classify samples ramdomly. For example, AUC is 0.7 means there is 70% chance that model will be able to distinguish between positive class and negative class.

Relation between TPR and FPR

As we know FPR is 1 - specificity, so when we increase TPR, FPR also increases and vice versa.

Achievement by Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn import metrics
from sklearn.metics import f1_score
import numpy as np

# True lables
y_true = np.array([1, 1, 2, 2])  
# Probability estimates of the positive class
y_scores = np.array([0,1, 0.4, 0.35, 0.8])
auc_score = metrics.roc_auc_score(y_true, y_scores)
>>>print(auc_score)
0.75

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
>>>print(f1_score(f1_score(y_true, y_pred, average='micro')))
0.33...

Reference

0%